令和6年1月7日
 [流れ星]
[流れ星]
第434回数学的な連続応募解答
<解答募集期間:12月10日〜1月7日>
「2024の問題]

追加問題(出題者は「ジョーカー」)
今回から2024に関する問題シリーズを載せます。
問題1

問題2
2024を2つの有理数に,次のように分ける。
どちらも整数でなく,一方は有理数,他方は1を加えると有理数になる。
2数の分け方の一例を求めよ。
上記の問題は文章の間違いでした。
ごめんなさい。またまた、私の不注意でした。下記のとおりです。
今までの労力には深くおわびします。12月22日に訂正しました。

問題3
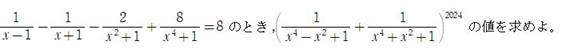
ごめんなさい。私が不注意でした。下記のとおりです。
今までの労力には深くおわびします。12月18日に訂正しました。
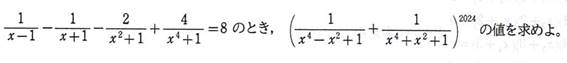
問題4(第427回からの「確率等」の問題シリーズの8問目)。

今回問題の作成にあたり、私の不注意で皆様に多大なご迷惑をおかけしたことを深くお詫び申し上げます。
で、早い応募順と競ってはいません、それぞれその時に頂いた解答を掲載します。
NO1「ジョーカー」 12/10
21時45分 受信 更新 1/7
寄せられた問題の解答です
NO2「スモークマン」 12/14
22時48分 受信 更新 1/7
(1)
2024=2^3*11*23
(11)
S(0)=4*2*2=16
(12)
S(1)= (1+2+2^2+2^3)(1+11)(1+23)=4320
(13)
S(-1)=(1+1/2+1/2^2+1/2^3)(1+1/11)(1+1/23)= 540/253
(14)
S(2)/S(1)
=(1+2^2+2^4+2^6)(1+11^2)(1+23^2)/4320
=5496100/4320
=274805/216
(15)
lim[m→∞]S(m+1)/S(m)
=lim[m→∞](1+2^(m+1)+(2^2)^(m+1)+(2^3)^(m+1))(1+11^(m+1))(1+23^(m+1)
/(1+2^m+(2^2)^m+(2^3)^m)(1+11^m)(1+23^m)
=lim[m→∞](1/(2^3)^m+2/2^3+2^2/2^3+2^3)(1/11^m+11)(1/23^m+23)/(1/2^m+23)
=(1/4+1/2+2^3)*11*23/1
=8855/4
(16)
Σ[k=1,n]1/(a(k)+√2024)
約数を小さい順に並べると
1,2,2^2,2^3,11,22,23,…,1012,2024
両端の積=2024
1/(a(k)+√2024)+1/(a(n-k)+√2024)
=1/(√a(k)(√a(k)+√a(n-k))+1/(a(n-k)(√a(k)+√a(n-k))
=2/(√a(k)+√a(n-k))
So…
2*{1/(√1+√2024)+1/(√2+√(2024/2)+1/(√4+√(2024/4))+1/(√8+√(2024/8))+1/(√11+√(2024/11))+1/(√22+√(2024/22))+1/(√23+√(2023/23))+1/(√(4*11)+√(2024/(4*11)))
=2{1/(1+√2024)+√2/(2+√2024)+√4/(4+√2024)+√8/(8+√2024)+√11/(11+√2024)+√22/(22+√2024)+√23/(23+√2024)+√44/(44+√2024)}
={(138(16389395+1545950√2+10364195√11+7853126√22)+6√23(176638165+121197010√2+31646533√11+16772410√22))/(18088488000+803516165√506)}
≒0.840756
(2)
36!
6*5*4*3*2*(9*8*7*6*5*4*3*2)^3
≡6*4*3*(9*8*7*6*4*3)^3
≡2^3*3^2*(3^4*7*2^6)^3
≡2^21*3^14*7^3
2-4-8-6-2…2^5≡2・・・2^21≡2^4*2≡2
3-9-7-1-3…3^5≡3・・・3^14≡3^2*3≡7
7-9-3・・・7^3≡3
So…36!の下の桁で最初の0でない数=2
(3)
(31)a(2b^2+c^2)=2024=2^3*11*23
2b^2≡0,2, c^2≡0,1
So…3<=2b^2+c^2≡0,1,2,3・・・4,8,44,88,92,184,1024,2024,11,22,23,46
4…なし
8…なし
11…9+2*1^2…(a,b,c)=(184,1,3)
22…4+2*3^2…(a,b,c)=(92,3,2)
23…なし
44…36+8=2*2^2+6^2…(a,b,c)=(46,2,6)
46…なし
88…16+2*6^2…(a,b,c)=(23,6,4)
92…なし
184…なし
1024…なし
2024…なし
結局
(a,b,c)=(22,3,8),(46,2,6),(184,1,3)
(32)a(a^2+b^2+c^2)=2024=2^3*11*23
3<=a^2+b^2+c^2≡0,1,2,3
2024^(1/3)<12
a=1,2,4,8,11
a=1…b^2+c^2=2023…なし
a=2…b^2+c^2=1008…16b’^2+16c’^2=1008…なし
a=4…b^2+c^2=490…b,cは4k±1
b=3,5,7,9,11,13,15,17,19,21
b=7,c=21以外ない
a=8…b^2+c^2=189…4k,4k±1
b=4,8,12…いずれもなし
a=11…b^2+c^2=63…なし
結局
(a,b,c)=(4,7,21),(4,21,7)
ジョーカーさんの追加問題
問題1
k+l-1=n
{n(n+1)/2}^2-{(k-1)k/2}^2=2024
(n(n+1))^2-((k-1)k)^2=8096
(n(n+1)>=8096^(1/2)=89.9…
So…n>=9
n=9
90^2-8096=4=(k(k-1))^2…k=2
2+l-1=9…l=8
(k,l)=(2,8)
n>=10以上の時はわからない…^^;
問題2
2024を2つの有理数に,次のように分ける。
どちらも整数でなく,一方は有理数,他方は1を加えると有理数になる。2数の分け方の一例を求めよ。
a+(b-1)=2024
(q/p)+(r/p)=2024
(q+r)=2024*(1+4)
2024/5+4*2024/5
問題3
2/(x^8-1)+1/(x^4+1)=2
1/(x^4-1)=2
1/2=x^4-1
x^4=3/2
{1/(x^4-x^2+1)+1/(x^4+x^2+1)}^2
=4(x^4+1)^2/(x^8+x^4+1)^2
=4*(25/4)/(9/4+5/2)^2
=25*4/(19^2)
=400/361
So…
与式=(400/361)^1012=(20/19)^2024
問題4
(1)
1-(2023-n)(2022-n)/(2023*2022)>1/2
(4045-√8181013)/2=592.376…<n
So…Min{n}=593
(2)
1-(2023-n)(2022-n)(2021-n)/(2023*2022*2021)>1/2
Min{n}=418
(3)
1-(2023-n)(2022-n)(2021-n)(2020-n)/(2023*2022*2021*2020)>1/2
(4043-√(5+4√8349581752261))/2=321.6…<n
Min{n}=322
「スモークマン」 12/19
22時57分 受信 更新 1/7
追加問題1
k+l-1=n
{n(n+1)/2}^2-{(k-1)k/2}^2=2024
(n(n+1))^2-((k-1)k)^2=8096
(n(n+1)+k(k-1))(n(n+1)-k(k-1))=8096=2^5*11*23
偶奇は同じ,and 奇数±奇数は偶数なので…
それぞれ、4の倍数
(2^3*11*23)x(2^2)
(2^2*11*23)x(2^3)
(2^3*23)x(2^2*11)
(2^2*23)x(2^3*11)
(n(n+1)>=8096^(1/2)=89.9…
So…n>=9
n(n+1)>=9*10
so…
(1) n(n+1)=2^2*11*23+2, k(k-1)=2^2*11*23-2…なし
(2) n(n+1)=2*11*23+2^2,k(k-1)=2*11*23-2^2…なし
(3) n(n+1)=2^2*23+2*11,k(k-1)=2^2*23-2*11…なし
(4) n(n+1)=2*23+2^2*11, k(k-1)=2*23-2^2*11…(n,k,l)=(9,2,8),(9,-1,11),(-10,-1,-8),(-10,2,-11)
lは自然数なので
求めるものは…
(k,l)=(2,8),(-1,11)
だけね ^^
問題2
2024を2つの有理数に,次のように分ける。
どちらも整数でなく,一方は有理数,他方は1を加えると有理数になる。2数の分け方の一例を求めよ。
a+(b-1)=2024
(q/p)+(r/p)=2024
(q+r)=2024*(1+4)
2024/5+4*2024/5
問題3
与式
=2/(x^2-1)-2/(x^2+1)+4/(x^4+1)
=4/(x^4-1)+4/(x^4+1)
=8/(x^8-1)
=8
So…
x^8-1=1
x^8=2
so…x^4=±√2
1/(x^4-x^2+1)+1/(x^4+x^2+1)
=(x^2+1)/(x^6-1)+(x^2-1)/(x^6+1)
=2(x^8+1)/(x^12-1)
=6/(±2√2-1)
この2024乗は計算できません…^^;
水の流れ:困惑させてごめんなさい。>
「スモークマン」 12/23
16時50分 受信 更新 1/7
問題2
回答
x^2+y=2024
y+1=z^2
x^2+(z^2-1)=2024
x^2+z^2=2025=5*405=5^2*81=5^2*9^2*(5^2+12^2)/13^2・・・例えば..13^2=5^2+12^2
x^2=(5^2*9/13)^2=50625/169
z=5*9*12/13
y=(5*9*12/13)^2-1=291431/169
つまり、例えば
50625/169+291431/169=2024
とか、いくらでもあり得ますね ^^
「スモークマン」 12/23
19時05分 受信 更新 1/7
問題1の5、6の再考したものです ^^
問題1
(5)
lim[m→∞]S(m+1)/S(m)
2024=2^3*11*23
S(m)
=(1+2^m+2^(2m)+2^(3m))(1+11^m)(1+23^m)
lim[n→∞]S(m+1)/S(m)
=lim[n→∞]
(1+2^(m+1)+2^(2m+2)+2^(3m+3))(1+11^(m+1))(1+23^(m+1)
/{(1+2^m+2^(2m)+2^(3m))(1+11^m)(1+23^m)}
=(0+0+0+2^3)(0+11)(0+23)/{(0+0+0+1)(0+1)(0+1))
=2^3*11*23
=2024
(6)
Σ[k=1,16]1/(a(k)+√2024)
例えば…
1/(1+√2024)+1/(2024+√2024)
=1/(1+√2024)+1/((√2024)*(1+√2024))
=(1/(1+√2024))(1+1/√2024))
=1/√2024
一般に…
1/(a(k)+√2024)+1/(2024/a(k)+√2024)
=1/(a(k)+√2024)+a(k)/(√2024*(a(k)+√2024))
=1/√2024
So…
与式
=(16/2)*(1/√2024)
=8/√2024
=2√506/253
綺麗な答えになるものですね♪
問題3
(1)a(2b^2+c^2)=2024=2^3*11*23
2b^2≡0,2, c^2≡0,1
So…3<=2b^2+c^2≡0,1,2,3・・・4,8,44,88,92,184,1024,2024,11,22,23,46
4…なし
8…なし
11…9+2*1^2…(a,b,c)=(184,1,3)
22…4+2*3^2…(a,b,c)=(92,3,2)
23…なし
44…36+8=2*2^2+6^2…(a,b,c)=(46,2,6)
46…なし
88…16+2*6^2…(a,b,c)=(23,6,4)
92…なし
184…なし
1024…なし
2024…なし
結局
(a,b,c) = (23,6,4)
,(46,2,6), (92,3,2) ,(184,1,3)
追加問題1
k+l-1=n
{n(n+1)/2}^2-{(k-1)k/2}^2=2024
(n(n+1))^2-((k-1)k)^2=8096
(n(n+1)+k(k-1))(n(n+1)-k(k-1))=8096=2^5*11*23
偶奇は同じ,and 奇数±奇数は偶数なので…
それぞれ、4の倍数
(2^3*11*23)x(2^2)
(2^2*11*23)x(2^3)
(2^3*23)x(2^2*11)
(2^2*23)x(2^3*11)
(n(n+1)>=8096^(1/2)=89.9…
So…n>=9
n(n+1)>=9*10
so…
(1) n(n+1)=2^2*11*23+2, k(k-1)=2^2*11*23-2…なし
(2) n(n+1)=2*11*23+2^2,k(k-1)=2*11*23-2^2…なし
(3) n(n+1)=2^2*23+2*11,k(k-1)=2^2*23-2*11…なし
(4) n(n+1)=2*23+2^2*11, k(k-1)=2*23-2^2*11…(n,k,l)=(9,2,8),(9,-1,11),(-10,-1,-8),(-10,2,-11)
lは自然数なので
求めるものは…
(k,l)=(2,8),(-1,11)
だけね ^^
「問題2
回答
x^2+y=2024
y+1=z^2
x^2+(z^2-1)=2024
x^2+z^2=2025=5*405=5^2*81=5^2*9^2*(5^2+12^2)/13^2・・・例えば..13^2=5^2+12^2
x^2=(5^2*9/13)^2=50625/169
z=5*9*12/13
y=(5*9*12/13)^2-1=291431/169
つまり、例えば
50625/169+291431/169=2024
<水の流れ:訂正前の問題の答えです。>
NO3「kasama」
12/17
00時08分 受信 更新 1/7
寄せられた問題の1回目の解答です
<コメント:追加問題2の解法方針を立てたいです。問題文を次のように解釈するのでしょうか?
a,bを整数でない有理数としたとき、 a+√(b+1) = 2024
となるような組みを求めれば良いのでしょうか。例えば、
6068/3+√(7/9+1) = 2024 などが考えられます、>
「kasama」
12/19
00時06分 受信 更新 1/7
寄せられた問題の2回目の解答です
<コメント:追加問題2は未だできていません。問題文は次のように、赤字を補えば、文章は成り立ちます。しかし、その解釈でいくと、
例えば、a=2023/2,b=2025/2です。ちょっと簡単過ぎるので、違うのだろうと思います。もう少し悩んでみます。
2024を2つの有理数a,bに,次のように分ける。
どちらも整数でなく,一方は有理数a,他方はaに1を加えると有理数bになる。2数の分け方の一例を求めよ。>
「kasama」
12/25
00時31分 受信 更新 1/7
寄せられた問題の3回目の解答です
<コメント:追加問題2についてです。いろいろ悩みましたが、円周上の有理点を求める方針でアプローチしました。大分前に出題された楕円関数上の有理点を求める問題を思い出しました。初等数学では歯が立たず、いろんな文献を参考にして、解答を作った覚えがあります。あれから20年ほど経ちますが、数学力は上がっていませんが、年齢だけはしっかり上がりました。>
NO4「よふかしのつらいおじさん」12/21 21時18分 受信 更新 1/7
寄せられた問題の1回目の解答です
NO4「よふかしのつらいおじさん」12/27 18時15分 受信 更新 1/7
寄せられた問題の2回目の解答です
NO5「二度漬け白菜」 01/01
14時51分 受信 更新 1/7
[問題 1]
2024を素因数分解すると,2024=(2^3)*11*23.
このことから,S(x)は次式で計算できることがわかる.
S(x)=(1+2^x+4^x+8^x)*(1+11^x)*(1+23^x).
(1) S(0)=4*2*2=16. (答)
(2) S(1)=(1+2+4+8)*(1+11)*(1+23)=4320. (答)
(3) S(-1)=(1+1/2+1/4+1/8)*(1+1/11)*(1+1/23)=540/253. (答)
(4) S(2)/S(1)=(1+2^2+4^2+8^2)*(1+11^2)*(1+23^2)/4320=274805/216. (答)
(5)
任意の正の実数 m に対して,不等式
2024^m < S(m) < 15*1012^m + 2024^m
が成り立つ.よって,
2024^(m+1)/(15*1012^m + 2024^m) < S(m+1)/S(m) < (15*1012^(m+1) + 2024^(m+1))/(2024^m)
つまり,
2024/(15*(1/2)^m + 1) < S(m+1)/S(m) < (15*1012*(1/2)^m + 2024).
ここで,
lim[m→∞](2024/(15*(1/2)^m + 1))=2024,
lim[m→∞](15*1012*(1/2)^m + 2024)=2024
であるから,
lim[m→∞]S(m+1)/S(m)=2024. (答)
(6)
(与式)
=Σ[k=1..8]1/(a[k]+√(2024)) + Σ[k=1..8]1/(a[17-k]+√(2024))
=Σ[k=1..8]1/(a[k]+√(2024)) + Σ[k=1..8]1/(2024/a[k]+√(2024))
=Σ[k=1..8]1/(a[k]+√(2024)) + Σ[k=1..8](a[k]/√(2024))*(1/(a[k]+√(2024)))
=(1/√(2024))*Σ[k=1..8](a[k]+√(2024))/(a[k]+√(2024))
=(1/√(2024))*Σ[k=1..8](1)
=8/√(2024)
=4/√(506). (答)
[問題 2]
36!を1の位からみていくとき,最初に現れる0でない数字は 2 (答)
floor(36/5)+floor(36/5^2)=7+1=8 であるので,
36!の末尾には 0 が8個続く.
求める値は,36!/(10^8) を 10 で割った余りである.
(36!/10^8)
≡(1/2^8)*(1*2*3*4*6*7*8*9*2)^3*(1*2*3*4*6)(mod 10)
≡(1/2^8)*(2^8*3^4*7)^3*(2^4*3^2)(mod 10)
≡(3^4*7)*(2^8*3^4*7)^2*(2^4*3^2)(mod 10)
≡(1*7)*(6*1*7)^2*(4)(mod 10)
≡(7)*(2)^2*(4)(mod 10)
≡2(mod 10).
[追加問題 1]
問題文の条件を満たす k,l の組は,
(k,l)=(-1,11)および(2,8). (答)
k^3+(k+1)^3+(k+2)^3+ … +(k+l-1)^3=2024 ---(★)
まず,k≧0の場合を考える.
2024≡2(mod 3)である.
また,0^3≡0(mod 3),1^3≡1(mod 3),2^3≡2(mod 3)である.
よって(★)を満たすような k は k≡2(mod 3) に限られる.
(k≡0(mod 3) だとすると,
k^3+(k+1)^3+(k+2)^3+ … (有限和)
≡0+1+2+0+1+2+ …
≡0(mod 3) or 1(mod 3)
となるから,これら有限項の和が2024になることはあり得ない.
k≡1(mod 3) の場合も同様)
よって,k=2,5,8,11の可能性しかない.
(★)は次のように変形できる.
((k+l-1)*(k+l)/2)^2 = 2024+(k*(k-1)/2)^2 --- (★★)
ここで,((k+l-1)*(k+l)/2)^2 は平方数.
k=2,5,8,11のうち,2024+(k*(k-1)/2)^2 が平方数となるのは
k=2のみである.
k=2のとき,(★★)より l=8.
k<0の場合には,k=-p (p>0) とおくと,(★)は次のようになる.
(-p)^3+(-p+1)^3+(-p+2)^3+ … +(-p+l-1)^3=2024
よって,
(-p)^3+(-p+1)^3+(-p+2)^3+ … +(p)^3+(p+1)^3+(p+2)^3+ … +(p+(l-1-2*p))^3=2024
つまり,
(p+1)^3+(p+2)^3+ … +(p+1+(l-2*p-1)-1)^3=2024 --- (★★★)
k<0の場合は,(★★★)を満たす2つの正整数 p+1, l-2*p-1 を探す問題に帰着できる.
[追加問題2]
分け方の一例は,
(216/5)^2 と -1+(63/5)^2. (答)
nを任意の正整数として,
x=(45*(2025*n^2-1)/(2025*n^2+1))^2
y=-1+(4050*n/(2025*n^2+1))^2
とすれば,x,yはいずれも整数ではない有理数であって,
x,y+1は有理数の平方,x+y=2024.
<水の流れ:訂正前の問題の答えです。>
[追加問題 3]
条件式:
1/(x-1)-1/(x+1)-2/(x^2+1)+4/(x^4+1)=8
の分母を払って整理すると,x^4+1=x^8.
よって,
(1/(x^4-x^2+1)+1/(x^4+x^2+1))^(2024)
=(2*(x^4+1)/(x^8+x^4+1))^(2024)
=(2*x^8/(x^8+x^8))^(2024)
=(1)^(2024)
=1. (答)
[追加問題 4]
(3) 求めるnの最小値は,322. (答)
このくじから4本を同時に取り出すとき,少なくとも1本が当たり
である確率は,1-(2023-n)*(2022-n)*(2021-n)*(2020-n)/(2023*2022*2021*2020).
f(n)=(2023-n)*(2022-n)*(2021-n)*(2020-n)/(2023*2022*2021*2020)
とおくと,f(0)=1,f(2020)=0であり,区間(0,2020)でf(n)は単調減少.
f(321)-1/2>0,
f(322)-1/2<0
である.
[問題 3] に関しては,しらみつぶしに解を調べる方法しか考えつかず,
解答を断念しました.
NO6「三角定規」 01/05
20時52分 受信 更新 1/7
寄せられた問題の解答です
<コメント:今回の問題1(6), 有理化まではすぐ見えましたが,その後が見えず後回しに。最後に16項すべてを書き出してみたら,うまく消えたり整理したりできることに気がつきました。>
「水の流れ」


皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。
