令和７年７月２０日

[流れ星]

　　第456回数学的な連続応募解答

　　　＜解答募集期間：6月22日〜7月20日＞

［高次方程式］

　

　

追加問題（出題者は「ジョーカー」）　新作シリーズ

四分円内の正方形と正三角形の1辺について『１』　

問題１　　シリーズ7問目

正方形と正三角形の1辺が等しいとき(辺を共有する),

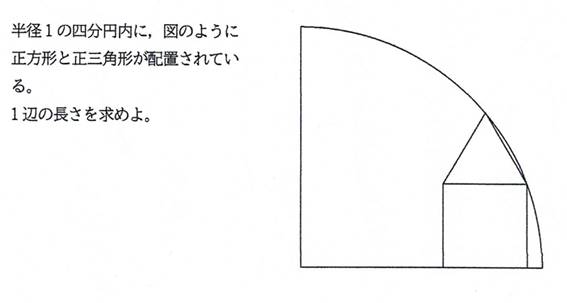
問題２　シリーズ8問目

正方形と正三角形の1辺が等しいとき(辺を共有する),

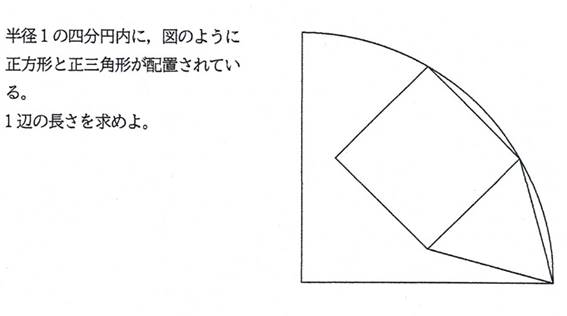
NO1「ジョーカー」 　 06/22 　　 11時30分 受信 更新 7/20

寄せられた解答です

NO2「スモークマン」 06/24 20時00分　 受信 更新 7/20

(1)

x^2024+2*x^2023+3*x^2022+…+2024*x+2025=0

これをx^2024 で割った方程式

1+2/x+3/x^2+…+2024/x^2023+2025/x^2024=0

という方程式の解は1/α1,1/α2,…,1/α2024であるから、

解と係数の関係式より

2025*t^2024+2024*t^2023+…+2*t+1=0

2025*(1+t)^2025+2024*(1+t)^2024+…+2*(1+t)+1=0

の解t=1-1/x である。

So…

(1/2025)Σ[k=1,2025]k=2025*2026/(2*2025)=1013

(2)

x^2025=10x+4

この方程式の解をα(k)…k=1〜2025 とすると、

Σ[k=1,2025]α(k)^2025=Σ[k=1.2025](10α(k)+4)

解と係数の関係よりΣ[k=1.2025]α(k)=0 なので、

求めるものは

2025*4=8100

(3)

x^11+x^4+x^3+x^2+x+1=0

は、明らかに-1を根に持つ

また、ωも持つ。

So…

与式

x^11+x^5+x^4+x^3+x^2+x+1-x^5

=(x^3+1)(x^2+1+1)+x^5(x^6-1)

=(x^3+1)(x^2+x+1)+x^5(x^3-1)(x^3+1)

=(x^3+1)(x^2+x+1)+x^5(x^3+1)(x-1)(x^2+x+1)

=(x^3+1)(x^2+x+1)(1+x^6-x^5)

=(x+1)(x^2-x+1)(x^2+x+1)(x^6-x^5+1)

追加問題１

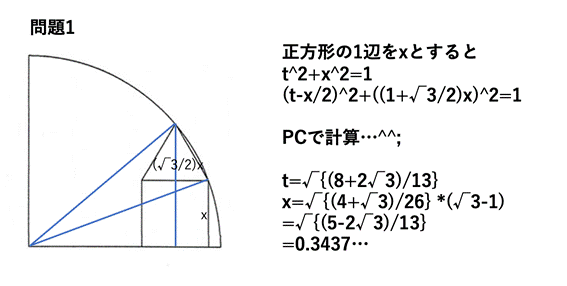
追加問題２

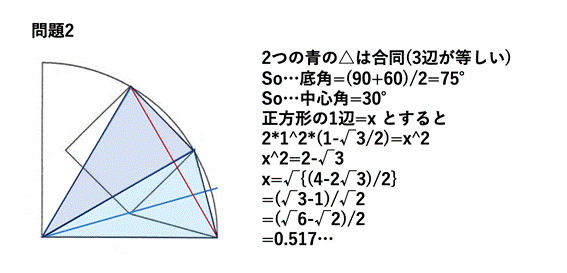
NO3「よふかしのつらいおじさん」 06/28 20時34分 受信 更新 7/20

寄せられた解答です

NO4「kasama」 07/01 00時23分　　 受信 更新 7/20

寄せられた解答です

NO5「浜田明巳」　　　　07/03 17時44分　 受信 更新 7/20

寄せられた解答です

「浜田明巳」　　　　07/08 17時28分　 受信 更新 7/20

　設問３の因数分解の考察です。

NO6「三角定規」 07/04 20時53分　 受信 更新 7/20

寄せられた解答です

NO7「二度漬け白菜」 07/13 18時54分　 受信 更新 7/20

第456回の応募問題の解答：

[設問1]

Π[k=1〜2024](1-1/α[k])=1013 (答)．

P(x)=Σ[j=0〜2024](2025-j)*x^(j)

とおく．

k=1,2,…,2024に対して，P(α[k])=0 である．

ここでさらに，F(x)=(x^2024)*P(1/x) とおく．

F(x)

=(x^2024)*P(1/x)

=(x^2024)*Σ[j=0〜2024](2025-j)*x^(-j)

=Σ[j=0〜2024](2025-j)*x^(2024-j)

=Σ[j=0〜2024](1+j)*x^(j)

である．

F(x)は x についての2024次の多項式であって，x^2024の係数は2025.

さらに，k=1,2,…,2024に対して，

F(1/α[k])=((1/α[k])^2024)*P(α[k])=0

となっている．

つまり，x=1/α[k] は， F(x)=0 の解となっている．

よってF(x)は次のように因数分解できる．

F(x)=2025*Π[k=1〜2024](x-1/α[k]).

この等式にx=1を代入して，

F(1)=2025*Π[k=1〜2024](1-1/α[k]).

よって，

Π[k=1〜2024](1-1/α[k])=F(1)/2025=1013.

[設問2]

Σ[k=1〜2025]α[k]^2025 = 8100 (答)

x^2025-10*x-4=Π[k=1〜2025](x-α[k])

が成り立っている．

両辺のx^2024の係数を比較して，

0=-(Σ[k=1〜2025]α[k]).

よって，

Σ[k=1〜2025]α[k]^2025

=Σ[k=1〜2025](10*α[k]+4)

=10*Σ[k=1〜2025]α[k] + Σ[k=1〜2025](4)

=10*0+4*2025

=8100.

[設問3]

(x^11+x^4+x^3+x^2+x+1)=(x+1)*(x^2-x+1)*(x^2+x+1)*(x^6-x^5+1) (答)

(x^11+x^4+x^3+x^2+x+1)

=(x+1)*(x^10-x^9+x^8-x^7+x^6-x^5+x^4+x^2+1)

=(x+1)*(x^6*(x^4+x^2+1)-x^5*(x^4+x^2+1)+(x^4+x^2+1))

=(x+1)*(x^4+x^2+1)*(x^6-x^5+1)

=(x+1)*((x^2+1)^2-x^2)*(x^6-x^5+1)

=(x+1)*(x^2+1-x)*(x^2+1+x)*(x^6-x^5+1)

[追加問題1]

一辺の長さは，(1/13)*(65-26*3^(1/2))^(1/2) (答)

一辺の長さをsとすると，

((3^(1/2))*s+s)^2+s^2=1^2.

これを解いて，

s=(1/(5+2*3^(1/2)))^(1/2)=(1/13)*(65-26*3^(1/2))^(1/2).

[追加問題2]

一辺の長さは，(1/2)*(6^(1/2)-2^(1/2))(答)

一辺の長さをtとすると，

|(-t)*(cos(-75°)+i*sin(-75°))+1|=1.

これを解いて，

t=2*cos(-75°)=(1/2)*(6^(1/2)-2^(1/2)).

＜水の流れ：応募者全員へ　猛暑中エアコン等をつけての解答と入力に大変な労力をおかけしましたことを厚く御礼申し上げます。次回の「定積分」もよろしくお願いします。＞

水の流れ　　　　　　　　　　　　　　　　　　　　　更新　7月20日

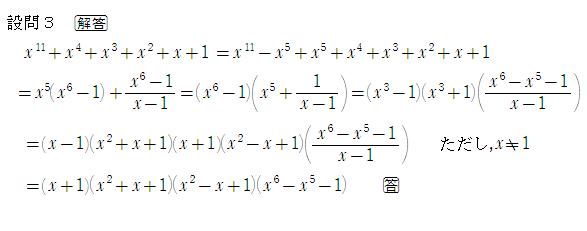
皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。