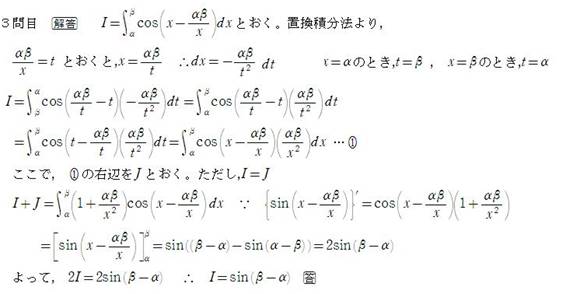令和７年８月１７日

[流れ星]

　　第457回数学的な連続応募解答

　　　＜解答募集期間：7月20日〜8月17日＞

［定積分］

　

　

追加問題（出題者は「ジョーカー」）　新作シリーズ

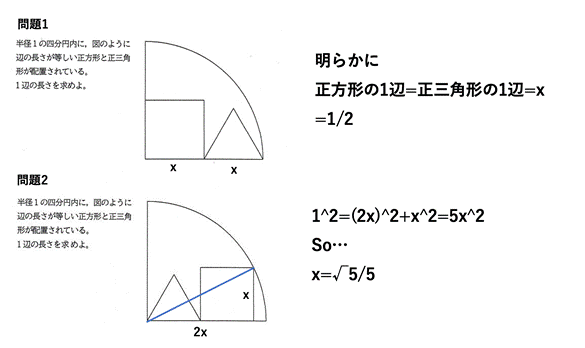
四分円内の正方形と正三角形の1辺について『２』　

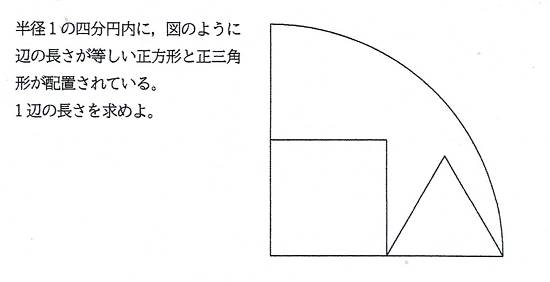
問題１　　シリーズ１問目

正方形と正三角形の1辺が等しいとき(辺を共有しない),

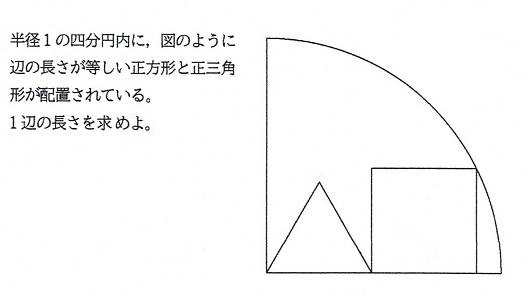
問題２　シリーズ２問目

正方形と正三角形の1辺が等しいとき(辺を共有しない),

NO1「ジョーカー」 　 07/20 　　 16時55分 受信 更新 8/17

寄せられた解答です

「ジョーカー」 　 07/21 　　 22時47分 受信 更新 8/17

寄せられ３問目の解答です

「ジョーカー」 　 07/22　　 17時06分 受信 更新 8/17

寄せられ2問目の補足解法です

NO2「浜田明巳」　　　　07/22 12時15分　 受信 更新 8/17

寄せられた解答です

NO3「kasama」 07/27 23時48分　　 受信 更新 8/17

寄せられた解答です

N04「三角定規」 07/28 14時55分　 受信 更新 8/17

寄せられた解答です

NO5「よふかしのつらいおじさん」 07/31 20時58分 受信 更新 8/17

寄せられた解答です

NO6「二度漬け白菜」 08/10 11時35分　 受信 更新 8/17

第457回の応募問題の解答：

[設問1]

(与式)=log(2+5^(1/2))　(答)

(d/dx)log(x+(x^2+1)^(1/2)) = (x^2+1)^(-1/2)

であることに注意する．

∫_[x=0,2]((x^2+1)^(-1/2))dx

=[log(x+(x^2+1)^(1/2))]_[0,2]

=log(2+5^(1/2)).

[設問2]

(与式)=(1/2)*(log(1+2^(1/2))+2^(1/2)) (答)

(与式)

=∫_[x=0,Pi/4]((cos(θ))^(-3))dθ

=∫_[t=0,(1/2)^(1/2)]((1-t^2)^(-2))dt ( t=sin(θ)と置換 ) =(1/4)*∫_[t=0,(1/2)^(1/2)](1/(1+t)+1/(1-t)+1/(1+t)^2+1/(1-t)^2)dt

=(1/4)*[log(1+t)-log(1-t)-1/(1+t)+1/(1-t)]_[0,(1/2)^(1/2)]

=(1/2)*(log(1+2^(1/2))+2^(1/2)).

[設問3]

(与式)=sin(β-α) (答)

(与式)=A とおく．

A=∫_[x=α,β](cos(x-α*β/x))dx

=∫_[t=β,α](cos(α*β/t-t)*(-α*β)/t^2)dt (t=α*β/x と置換)

=(α*β)*∫_[t=α,β](cos(t-α*β/t)/t^2)dt. よって，

2*A

=∫_[x=α,β](cos(x-α*β/x))dx + (α*β)*∫_[x=α,β](cos(x-α*β/x)/x^2)dx

=∫_[x=α,β](cos(x-α*β/x)*(1+(α*β)/x^2))dx

=[sin(x-α*β/x)]_[α,β]

=2*sin(β-α). よって，A=sin(β-α).

[追加問題1]

一辺の長さは，1/2 (答)

一辺の長さをsとすると，

s+s=1. よって，s=1/2.

[追加問題2]

一辺の長さは，(1/5)^(1/2)(答)

一辺の長さをtとすると，

(t+t)^2+t^2=1^2. よって，t=(1/5)^(1/2).

NO7「スモークマン」 08/13 22時23分　 受信 更新 8/17 <

追加問題

水の流れ　　　　　　　　　　　　　　　　　　　　　更新　８月１８日