令和６年３月３1日
[流れ星]
第438回数学的な連続応募解答
＜解答募集期間：３月３日〜３月３１日＞
「歴史上の定理］
問題１
互いに接する３個の甲乙丙の円径を六十九寸 , 四十六」寸 , 二十三寸とするとき,これらすべてに外接する小円の円径を求めよ。
答曰 六寸
文献 算法点竄初學抄 橋本昌方著
原典 デカルトの円定理
注 ルネ・デカルトは1643年にボヘミヤのエリザベス女王への手紙の中でこの問題を詳細に研究している。
江戸時代後半には、同じ考えの問題を和算の中に出てくる。
問題２
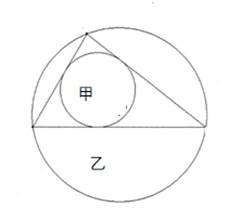三角形に内接する甲円と外接する乙円があり 甲の半径を四寸 乙円の半径を九寸とする。
甲円乙円の中心間の距離を求めよ。
原典 オイラー・チャップル定理
次の２問は大学入試問題にもありそうな問題
問題３
図のように三辺の長さが八、九、九である等面四面体ＯＡＢＣがある、次の値を求めよ。
（１）四面体ＯＡＢＣの体積
（２）四面体ＯＡＢＣ外接球の半径
（３）四面体ＯＡＢＣ内接球の半径
問題４
図のように三辺の長さが三、四、七である直方体の中に四面体ＤＥＦＧがある。
次の値を求めよ。
（１）四面体ＤＥＦＧの表面積
（２）四面体ＤＥＦＧの外接球の半径
（３）四面体ＤＥＦＧの内接球の半径
追加問題（出題者は「ジョーカー」）
今回から2024に関する問題シリーズ第4段で終了
問題１
問題２
NO1「ジョーカー」
3/3 21時53分 受信 更新 3/31
寄せられた問題の解答です
「ジョーカー」 4/1 19時55分 受信 更新 4/1
4月1日の午前に「日曜数学者」からの次のようなメールが届きました。
No.438追加問題1の出題者ジョーカーさんの解答を楽しみにしていたのですが、その中に、納得できない推論が１箇所がありました。
m,nは整数、-119<m<17のとき、
(m+1-n)((m+1)^2+(m+1)*n+n^2)=(m+119)*(m-17) ------- (*)
から
m+1-n=±1,±(m+119),±(m-17),±(m+119)*(m-17)
------ (**)
の8通りの場合分けをしていますが、これ以外の場合を除外できる根拠が
明示されていません。
一般的に、0でない整数a,b,c,dに対して、a*b=c*dならば、
aはc*dの約数ですが、a=±1,±c,±d,±c*dとは限りません。
(例えば、a=3,b=6,c=2,d=9のとき)
もちろん、実際に-119<m<17を満たす個々の整数mに対して調べることで、
(*)を満たす整数nが存在しないことが簡単に確認できるので、(**)は結果的に
正しいと分かります。
できれば、凡人の「日曜数学者」にも理解できるように、明確な根拠を追加
していただけないでしょうか？
「ジョーカー」からの訂正解答です。
＜コメント：日曜数学者さんからのご指摘で，別添のように解答を修正しました。「日曜数学者」さんには感謝です。＞
NO2「日曜数学者」 3/6 08時07分 受信 更新 3/31
[追加問題1の解答(訂正版)]
m,nは整数で、
n^3=m^3+2*m^2-99*m+2024 -----------(1)
とする。
(case 1) n=mのとき
(1)より、
2*m^2-99*m+2024=0 ------------(2)
でなければならないが、mは整数なので、
2*m^2-99*m+2024=2*(m-99/4)^2+6391/8 > 0
より、(2)は整数根mを持たない。
よって、(1)はm=nとなる整数解(m,n)を持たない。
(case 2) n!=mのとき
(1)より、
n^3-m^3=2*m^2-99*m+2024 --------(3)
ここで、mは整数なので、
2*m^2-99*m+2024=2*(m-99/4)^2+6391/8 > 0 -----(4)
(3),(4)より、
n^3-m^3>0
n^3>m^3
m,nは整数なので、
n>m
n>=m+1
n^3>=(m+1)^3
よって、
n^3-m^3>=(m+1)^3-m^3=3*m^2+3*m+1 ----------(5)
(3),(5)より、
2*m^2-99*m+2024>=3*m^2+3*m+1
m^2+102*m-2023<=0
(m+119)*(m-17)<=0
-119<=m<=17 ------------- (8)
ここで、(1)より、m^3+2*m^2-99*m+2024は、整数の３乗数でなければならない。
(8)を満たす整数m、つまり、m=-119,-118,-117, ... ,16,17に対して、
m^3+2*m^2-99*m+2024
の値が整数の3乗数になるのは、m=-119,17のときに限ることが、容易に確認できる。
m=-199のとき、(1)より、
n^3=(-119)^3+2*(-119)^2-99*(-119)+2024=-1643032=(-118)^3
nは整数なので、n=-118
である。
また、m=17のとき、(1)より、
n^3=17^3+2*17^2-99*17+2024=5832=18^3
nは整数なので、
n=18
である。
以上より、(1)の整数解(m,n)は、
(-119,-118), (17, 18)
であり、これに限る。
========================================
[追加情報(発展問題)]
m,nを有理数とするとき、
C: n^3=m^3+2*m^2-99*m+2024 -----------(1)
の解を求める。
３次曲線Cは、有理変換[m,n]→[u,v]
u=m-17
v=n-18
(逆変換[u,v]→[m,n]は、
m=u+17
n=v+18
)
により、３次曲線
C1: u^3 + 53*u^2 + 836*u + (-v^3 - 54*v^2 - 972*v)=0 ------ (2)
に写される。
３次曲線C1は、有理変換[u,v]→[U,V]
U=u-v
V=53*u-54*v
(逆変換[u,v]→[U,V]は、
u=54*U-V
v=53*U-V
)
により、３次曲線
C2: 8587*U^3 + (-321*V + 2862)*U^2 + (3*V^2 - 6372)*U + (-V^2 +
136*V)=0 ---------- (3)
に写される。
次の有理変換を求めるために、少し議論をする。
これをVの２次方程式と考えて、整理すると、
Φ1(U)*V^2+Φ2(U)*V+Φ3(V)=0 ------------ (4)
ここで、Φ1(U)=3*U - 1
Φ2(U)=-321*U^2 + 136
Φ3(U)=8587*U^3 + 2862*U^2 - 6372*U
である。
(3)をVの２次方程式と考えて、その判別式をD(U)とすると、
D(U)=Φ2(U)^2-4*φ1(U)*φ3(U)
=-3*U^4 + 4*U^3 + 600*U^2 - 25488*U + 18496
=-3*U^4 + 4*U^3 + 600*U^2 - 25488*U +136^2
D(U)はある有理数Ｗの平方数でなければならないので、
W^2=-3*U^4 + 4*U^3 + 600*U^2 - 25488*U +136^2
である。
実際に、
W=2*φ1(U)*V+Φ2(U)=2*(3*U-1)*V+(-321*U^2 + 136)
とすると、(2)より、
W^2-(-3*U^4 + 4*U^3 + 600*U^2 - 25488*U +136^2)
=(2*(3*U-1)*V+(-321*U^2 + 136))^2-(-3*U^4 + 4*U^3 + 600*U^2 - 25488*U +136^2)
=(36*U^2 - 24*U + 4)*V^2 + (-3852*U^3 + 1284*U^2 + 1632*U - 544)*V +
(103044*U^4 - 4*U^3 - 87912*U^2 + 25488*U)
=4*(3*U-1)*((3*U - 1)*V^2 + (-321*U^2 + 136)*V + (8587*U^3 +
2862*U^2 - 6372*U))
=0
となる。この有理変換の種明かしは、ここで終了。
つまり、３次曲線C2は、有理変換[U,V]→[Z,W}
Z=U
W=2*(3*U-1)*V+(-321*U^2 + 136)
(逆変換[Z,W]→[U,V]は、
U=W
V=(W-(-321*Z^2 + 136))/(2*(3*Z-1))
)
によって。楕円曲線
E0: W^2=-3*Z^4 + 4*Z^3 + 600*Z^2 - 25488*Z +136^2 --------(5)
に写される。
楕円曲線E0は、有理変換[Z,W]→[X,Y]
X=(272*W -24588*Z + 36992)/Z^2
Y=(73984*W -35011209/17*Z^2 - 6687936*Z + 10061824)/Z^3
(逆変換[X,Y}→{Z,W]は、
Z= (4624*X - 35011209)/(17*Y)
W=(21381376*X^3 - 323783660832*X^2 + (1932813504*Y + 1225784755641681)*X + (-10690688*Y^2 - 14634545317164*Y))/(78608*Y^2)
)
によって、楕円曲線、
E1: Y^2-6147/34*X*Y+1088*Y=X^3-35011209/4624*X^2+221952*X-1680538032
------(7)
に写される。
楕円曲線E1は、有理変換[X,Y]→[x,y]
x=1/4*X + 50
y=-6147/544*X + 1/8*Y + 135/2
(逆変換[x,y]→[X,Y]は。
X=4*x - 200
Y=(147*x + 136*y - 316530)/17
)
によって、楕円曲線
E: y^2=x^3-28491364 ----------------- (8)
に写される。
Eのねじれ点群は自明(無限遠点のみ)、Eのrankは4であり。Eの有理点群E(Q)の基底は、
P1=[1565, 61681]
P2=[2762, 145058]
P3=[11410/9, 1210238/27]
P4=[55465/144, 9249643/1728]
である。E(Q)はP1,P2,P3,P4から生成される。
E(Q)の各有理点から上記の逆変換を行って、(1)の有理点を求めることができる。
よって、３次曲線Cの有理点をいくつか求めると、以下のようになる。
[1286164766564652937213/184492798904572780337,
2231640512708723687538/184492798904572780337]
[-88290782218046522352877/4356862185789919517471,
-65963040699596875688402/4356862185789919517471]
[-496750565538888425/31503265150398083,
171652742668410342/31503265150398083]
[-254721191065315369/32897645889655715,
443266628289348166/32897645889655715]
[1630168443923568680454257171/63780842004231140619950591,
1655805148960890126391365262/63780842004231140619950591]
[73429646885341235690206820003/736410129209238586415724559,
73725646885902228693615262062/736410129209238586415724559]
[-130366393813/20192524066, 273227063883/20192524066] [-16091921853615944/1010241228045241, 4100043697652552/1010241228045241]
[-98577163/5219578, -67149603/5219578]
[66273832024/11134434493, 133315287884/11134434493] [16111261639058637565/1806927062653327238,
22800526659109959117/1806927062653327238]
[-732837555508750933048/30153705575748314615,
-621208186453538239088/30153705575748314615]
[-82969281159695/5200104662657, 19277383644978/5200104662657] [-2857695268265995685587/465846933604643902565,
6301984845984149711698/465846933604643902565]
[47113125677/891240301, 47364746298/891240301] [88665382363616633/2670131878307873, 89419230950375866/2670131878307873]
[-5333730359801915363473/1291870904473942143103,
17287897007192972797422/1291870904473942143103]
[-803491056441606663346876877/50110891647848929431308251,
73988197839686842421965838/50110891647848929431308251]
[-87365659388768/5445177339311, -7914693865842/5445177339311] [-2380087587642883/1473737218034372, 19123315810182469/1473737218034372]
[32814640/16352153, 200430102/16352153]
[-1830853735063/111545613440, -687470993303/111545613440] [-299445753259004608/5404473720478873, -291211856157037398/5404473720478873]
[102948830930213595500659/7257210955948865189188,
114005435393313350835419/7257210955948865189188]
[-709751/47953, 422714/47953]
[-3512593/321103, 4070622/321103]
[-45050535575/2789625257, -11350687182/2789625257] [464415074399/983849519735, 12349731775414/983849519735] [-1113064/66005, -535244/66005] [2796633145/845629658, 10199431857/845629658] [232/19, 272/19] [-59563/1558, -56283/1558] [-39163984455512/2887531920163, 31018589821556/2887531920163] [-193277567364553/15071864572126, 173049899854383/15071864572126] [-1897534972198243/131448123931365, 1250855352183842/131448123931365] [-3038285382783570725255/261494139988195170489,
3224912566327690297426/261494139988195170489]
[1644086753/155186073, 2074477946/155186073] [-168608199571021421/5637286028890467, -152973818132318474/5637286028890467]
[-1407141092072175533/80095110801732459,
-811979045221748258/80095110801732459]
[1817341245256250029887188279/401483997972126987624830871,
4800644915342632381020390254/401483997972126987624830871]
[-42983/48204, 618577/48204]
[-845983936/52674921, -123064246/52674921] [54640/2709, 56446/2709] [-1025445169/66777516, 489850727/66777516] [-1623393622023776/170511929706807, 2245813302411166/170511929706807] [-388345481/10040427, -367453634/10040427] [340183601/27701901, 397824962/27701901] [-1061/63, -506/63] [11699/3591, 43334/3591] [-428376703553/139546079235, 1846763796862/139546079235] [-3174418228614535/197912295471141, 52317208346114/197912295471141] [-37503222427370150569/2341313443470814335,
5516282586167137046/2341313443470814335]
[-87884338076494898255/17893750231082369601,
240897047399126363314/17893750231082369601]
[-119, -118]
[17, 18]
[-47099076121319689765444887639821519/1632941653565277829579911733961577,
-42356346803506232771397487915619174/1632941653565277829579911733961577]
[424150644357130174893927547959480868871/41074447305770457852239639364388038039,
543447610678452606105286435242161680286/41074447305770457852239639364388038039]
[-76637580295024/4857194260449, 26145145410926/4857194260449] [-8749697275376729/1139086666386792, 15354430768230871/1139086666386792]
[7376284639259200/76493693792241, 7406528769391834/76493693792241] [36762077973159163/1425487538741220, 37325688232865443/1425487538741220]
[-56382125140288272843510598878967/3515188589257818635306530095168,
-846480263888391384145768628599/3515188589257818635306530095168]
[-91562299820491543518015203069744/34734981502699641284546325287943,
457207573698451792149905630055274/34734981502699641284546325287943]
[-55060956777766572449/2906736202484751843,
-37689880237270625666/2906736202484751843]
[8369249027827773511492163/1394708113097297072767143,
16704226712955675298928246/1394708113097297072767143]
[5839229720966401410551/658865936192003235819,
8300918902002525164606/658865936192003235819]
[-59847222389754321560428523/2477028657367600344008289,
-50592419079993737582627318/2477028657367600344008289]
[-808742451656099887967992243169836440055/53158607403330039631785415287973678149,
413811753955759540986836588027549567666/53158607403330039631785415287973678149]
[-96519344905032282743141732432046732844379/9701635413465648056323367846380822554945,
126601157219001512837108021251199788076026/9701635413465648056323367846380822554945]
[-230872685015/18882100666, 225598416929/18882100666] [-15087553450675192/1074835521346375, 10896385705045308/1074835521346375]
[162561973759/11159993026, 178575020399/11159993026] [-439655210512274584/7302706538812867, -429176836544494704/7302706538812867]
[-74431270376784824496266401/4549886263747842850018862,
-26569037823632524007558249/4549886263747842850018862]
[1103676873266881513729364101062904/620598523783542204343540159283849,
7632022670421754074989165757519708/620598523783542204343540159283849]
[7231331/3514463, 43046014/3514463]
[-1752446339/106684001, -665266398/106684001] [-41903705/769699, -40715434/769699] [64096822871/4545072595, 71113563126/4545072595] [-24045874867552794803939/1737225294641088556609,
18071149133705546636066/1737225294641088556609]
[-1583891961269473115936431453/126838380223811050021578079,
1491158304603297338207232702/126838380223811050021578079]
[-6453814869703/52083577234, -6402526717983/52083577234] [207103733857096/12104031737359, 219022911631316/12104031737359] [-357189325624024/22125475848203, -88481201796896/22125475848203] [14539613263543/34731481690178, 436344384683271/34731481690178] [2295941199770592971476412600/29743102105652403561461557121,
375759262531163313688653330004/29743102105652403561461557121]
[-19076941390527966734134182269153/1183942268366926576785616452230,
-4211006753370289978952184120633/1183942268366926576785616452230]
[-10833589568053/4677234053887, 61303728689334/4677234053887] [-31506589843150795417793/1964259070253923623571,
-1211680488954576428722/1964259070253923623571]
[16677712779803/141797124991, 16739148673158/141797124991] [345986251925040212739743/14078550164448509495747,
352086011046044775941278/14078550164448509495747]
[-2916883067146730585768086451/185543161183914488039477465,
1065477035784668098828052634/185543161183914488039477465]
[-1449341553491786230122872673863081637415/180776497404346763874794921968042787333,
2430710431270693543367427314095224071362/180776497404346763874794921968042787333]
[34392016/3227795, 43250946/3227795]
[-15671183601715/519576870032, -14245165183187/519576870032] [-19121536/1090549, -10962702/1090549] [108882238483177/24314230536796, 290786738682113/24314230536796] [-1874984498562917438704/409718966584659349717,
5503129316460032822646/409718966584659349717]
[-3567660680848125244988925133373/222606406673942229742167089848,
440978260337580091336804931027/222606406673942229742167089848]
[-75541071240629/25578065627, -75523727434074/25578065627] [18381018217368557/917962377264773, 19003464110198002/917962377264773]
[-50422211357813/3287454670475, 24318043401462/3287454670475] [-358077106961820205/37379958473777867,
491755939958217598/37379958473777867]
[16098044989901927241705884947/1888490175458726755118488067,
23572652242189937618622748374/1888490175458726755118488067]
[-10513040982225088819231395070581787/451002794741825347711174807006109,
-8727980723936716311999301364176958/451002794741825347711174807006109]
「日曜数学者」 3/14 22時22分 受信 更新 3/31
[追加問題2の回答]
正整数nに対して、有理数係数の多項式
Σ_{k=1}^{2024}{(-x-x^2-...-x^n}^(k-1)}
のx^2023の係数をh(n)とする。
h(n)をn=1,2,3,4,...(nが小さい順)について、計算すると、
h(1)=-1
h(2)=-1
h(3)=0
h(4)=0
h(5)=-1
h(6)=1
となるので、h(n)=1となる最小のnは、6である。
[参考]
h(n)=1となるnで、2番目に小さいものは16、3番目に小さいものは118である。
h(7)=h(8)=h(9)=h(10)=h(11)=h(12)=h(13)=h(14)=h(15)=0
h(16)=1
17<=n<=117のとき、h(n)=0である。
h(118)=1
119<=n<=150のとき、h(n)=0である。
また、2000<=n<=2020のとき、h(n)=0である。
h(2021)=-1
h(2022)=1
h(2023)=0
[Pari/GPによる計算]
gp > f(n)=sum(i=1,n,-x^i)+O(x^2024);
gp > g(n)=sum(k=1,2024,f(n)^(k-1));
gp > h(n)=polcoeff(g(n),2023,x);
gp > h(1)
time = 1,381 ms.
%4 = -1
gp > h(2)
time = 12,520 ms.
%5 = -1
gp > h(3)
time = 42,626 ms.
%6 = 0
gp > h(4)
time = 1min, 16,177 ms.
%7 = 0
gp > h(5)
time = 1min, 44,986 ms.
%8 = -1
gp > h(6)
time = 2min, 7,158 ms.
%9 = 1
gp > h(7)
time = 2min, 27,173 ms.
%10 = 0
gp > h(8)
time = 2min, 46,304 ms.
%11 = 0
gp > h(9)
time = 2min, 57,579 ms.
%12 = 0
gp > h(10)
time = 3min, 5,649 ms.
%13 = 0
gp > h(11)
time = 3min, 15,108 ms.
%14 = 0
gp > h(12)
time = 3min, 26,178 ms.
%15 = 0
gp > h(13)
time = 3min, 32,320 ms.
%16 = 0
gp > h(14)
time = 3min, 40,231 ms.
%17 = 0
gp > h(15)
time = 3min, 45,628 ms.
%18 = 0
gp > h(16)
time = 3min, 45,739 ms.
%19 = 1
「日曜数学者」 3/15 13時27分 受信 更新 3/31
その後の調査で、
150<=n<=261のとき、h(n)=0,
h(288)=1
であることが確認できました。
このことにより、
nが2023=7*17^2の約数(1,7,17,7*17=119,17^2=289,7*17^2=2023)から1引いた数、
つまり、
0,6,16,118,288,2022
のとき、かつ、その時に限り、
h(n)=1
になると予想できます。この予想の証明に挑戦中です。
もしその証明ができたら、再度、応募します。
「日曜数学者」 3/16 14時38分 受信 更新 3/31
追加問題2(一般化したもの)を計算機を使わずに解きましたので、報告します。
追加問題2に関する以下の定理を証明できました。
[定理]
1<=n<=2023に対して、
Σ_{k=1}^{2024}{(-x-x^2-...-x^2)^(k-1)}のx^2023の係数をh(n)とすると、
h(n)は0,1,-1のいずれかの値をとる。
さらに、
h(n)=0 <===> not{(n+1)|2023} かつ not{(n+1)|2022}
h(n)=1 <===> (n+1)|2023 かつ not{(n+1)|2022}
h(n)=-1 <===> not{(n+1)|2023} かつ (n+1)|2022
である。
よろしくお願いいたします。
====================================
[追加問題2の解答]
有理係数の1変数xの多項式環Q[x]を単項イデアル(x^2024)で
割った商環をR=Q[x]/(x^2024)とする。
A(n),H(n)∈Rを
A(n)=-x-x^2-...-x^n
H(n)=Σ_{k=1}^{2024}{A(n)^(k-1)}
で定義する。
また、H(n)のx^2023の係数をh(n)とする。
x|A(n)より、
x^2024|A(n)^2024
よって、(Rの元として)
A(n)^2024=0
である。
H(n)=1+A(n)+A(n)^2+...+A(n)^2023
=(1-A(n)^2024)/(1-A(n))
=1/(1-A(n))
=1/(1+x+x^2+...+x^n)
=(1-x)/(1-x^(n+1))
=(1-x)*(1+x^(n+1)+x^(2*(n+1))+x^(3*(n+1))+...+x^([2023/(n+1)]*(n+1)))
H(n)の項の中で、x^2023の項に一致する可能性があるのは、
1*x^([2023/(n+1)]*(n+1)) ([2023/(n+1)]*(n+1)=2023のとき)
(-x)*x^([2023/(n+1)]*(n+1)) ([2023/(n+1)]*(n+1)=2022のとき)
のみである。
よって、1<=n<=2023に対して、H(n)のx^2023の係数h(n)は、
(n+1)|2023のとき、h(n)=1
not((n+1)|2023)かつ(n+1)|2022のとき、h(n)=-1
not((n+1)|2023)かつnot((n+1)|2022)のとき、h(n)=0
である。
2023=7*17^2 の約数は1,7,17,119,289,2023
2022=2*3*337の約数は1,2,3,6,337,674,1011,2022
なので、
n=6,16,118,288,2022のとき、h(n)=1
n=1,2,5,336,673,1010,2021のとき、h(n)=-1
not(n∈{1,2,5,6,118,288,336,673,1010,2021,2022})のとき、h(n)=0
である。
よって、h(n)=1となる最小のnは6である。
NO3「タカ」
3/6 10時06分
受信 更新 3/31
寄せられた問題の解答です
「タカ」 3/8 10時11分 受信 更新 3/31
寄せられた解法を載せておきます。
NO4「スモークマン」 3/13 23時37分 受信 更新 3/31
さて、今回もできたと思えるものだけの回答をば Orz
問題３
図のように三辺の長さが八、九、九である等面四面体ＯＡＢＣがある、次の値を求めよ。
（１）四面体ＯＡＢＣの体積
（２）四面体ＯＡＢＣ外接球の半径
（３）四面体ＯＡＢＣ内接球の半径
axaxbの直方体からaxaxbの直角三角錐を4個切り取ったもの
(1)
so…1-4/6=1/3
2a^2=8^2
a^2+b^2=9^2
b^2=9^2-32=49
so…(1/3)a^2*b=32*7/3=224/3
(2)
外接円の半径は直方体の対角線の半分
√(a^2+b^2+a^2)/2
=√(64+49)/2
=√113/2
(3)
内接円の半径rは
等面積の三角*r*4/3=224/3
当面積の△=4*√(9^2-4^2)=4√65
So…r=224/(16√65)=14√65/65
問題４
図のように三辺の長さが三、四、七である直方体の中に四面体ＤＥＦＧがある。
次の値を求めよ。
（１）四面体ＤＥＦＧの表面積
（２）四面体ＤＥＦＧの外接球の半径
（３）四面体ＤＥＦＧの内接球の半径
(1)
四面体DEFGの表面積
余弦定理からsinを求めて
FD=5
FE=√(3^2+7^2)=√58
DE=√(4^2+7^2)=√65
58+65-2*√(58*65)*cosθ=5^2
cosθ=49/√3770
sinθ=37√3770/3770
so…
底面積=√(58*65)*37√3770/3770*(1/2)=18.5
So…表面積=(3*4+(3+4)*7)/2+18.5=49
(2)
対角線の1/2が外接円の半径
対角線=√(3^2+4^2+7^2)=√74
So…外接円の半径=√74/2
「スモークマン」 3/19 17時11分 受信 更新 3/31
問題4
(3)
内接円の半径=(3*4*7/2)/49=6/7
追加問題1
n^3-1=m^3+2m^2-99m+2023
(n-1)(n^2+n+1)=m^3+2m^2-99m+2023
n-1 が右辺の約数
n^2+n+1-(n-1)=n^2+2>=3
2023=7*17^2
99=3^2*11
So…m=±1,7,17,7*17,17^2,7*17^2
n-1=±m
・n=m+1 のとき
m^2+102m-2023=0
(m+119)(m-17)=0
(n,m)=(-118,-119),(18,17)
・n=-m+1 のとき
f(m)=2m^3-m^2-96m+2023=0
f’(m)=6m^2-2m-96=0
3m^2-m-48=0
3(m-1/6)^2=48+1/12
(m-1/6)^2=16+1/36=(16*36+1)/36
m=(1+√577)/6
f((1+√577)/6)=(108377-577√577)/54=1750.31…>0
f(-11)=296>0
f(-12)=-425
so…整数解なし
結局…
(n,m)=(-118,-119),
(18,17)
NO5「二度漬け白菜」 3/16 11時36分 受信 更新 3/31
(追加問題の解答)
[追加問題 1]
(m,n)=(-119,-118), (17,18) (答)
n^3 = m^3+2*m^2-99*m+2024 ---(☆)
(m^3+2*m^2-99*m+2024)-(m^3)
=2*m^2-99*m+2024
=2*(m-99/4)^2+6391/8 > 0,
(m+25)^3-(m^3+2*m^2-99*m+2024)
=73*(m+1974/146)^2+18704/73 > 0.
よって，(m^3) < (m^3+2*m^2-99*m+2024) < (m+25)^3.
よって，(☆)を満たすnとして可能性があるのは，
n=m+1,m+2,...,m+24 の24個だけである．
n=m+k (kは1≦k≦24なる整数) とおく．
(☆)より，
(m+k)^3=m^3+2*m^2-99*m+2024.
よって，
(3*k-2)*m^2+(3*k^2+99)*m+k^3-2024=0 ---(☆☆)
mについての2次方程式(☆☆)が整数解をもつためには，
(3*k^2+99)^2-4*(3*k-2)*(k^3-2024)
が平方数であることが必要．
1≦k≦24なる整数kのうち，(3*k^2+99)^2-4*(3*k-2)*(k^3-2024)
が平方数となるのは，k=1のみ．
k=1のとき，(☆☆)から，
m=-119,17.
[追加問題 2]
問題文の条件を満たすような最小のnは，n=6(答)
無限級数 f(x) = Σ[k=0..∞]a[k]*x^k に対して，
f(x)の x^m の係数を [x^m]f(x) と記すことにする．
(つまり， [x^m]f(x)=a[m])
また，命題Pに対して，《P》を次のように決める．
Pが真のとき 《P》= 1,
Pが偽のとき 《P》= 0.
[x^2023]Σ[k=1..2024](-x-x^2-...-x^n)^(k-1)
=[x^2023]Σ[k=0..2023](-x-x^2-...-x^n)^k
=[x^2023]Σ[k=0..∞](-x-x^2-...-x^n)^k
=[x^2023]Σ[k=0..∞]((-x)*(1-x^n)/(1-x))^k
=[x^2023]1/(1-(-x)*((1-x^n)/(1-x)))
=[x^2023](1-x)/(1-x^(n+1))
=[x^2023](1-x)*(1+x^(n+1)+x^(2*(n+1))+x^(3*(n+1))+...)
=《a*(n+1)=2023となるような整数aが存在する》-《b*(n+1)+1=2023となるような整数bが存在する》---(★).
ここで，1≦n≦5のとき，
《a*(n+1)=2023となるような整数aが存在する》= 0，
《b*(n+1)+1=2023となるような整数bが存在する》≧ 0
であるから，(★)≦0.
n=6のとき，
《a*(n+1)=2023となるような整数aが存在する》= 1,
《b*(n+1)+1=2023となるような整数bが存在する》= 0
であるから，(★)=1.
以上より，問題文の条件を満たすような最小のnは，n=6(答)
一般には次のようになりました．
a,b,n を正整数とする．
xの多項式 Σ[k=0..b](-x-x^2-...-x^n)^k のx^aの係数を
F(a,b,n)とする．つまり，
F(a,b,n)=[x^a](Σ[k=0..b](-x-x^2-...-x^n)^k)
とする．
F(a,b,n)は以下のような計算式で計算できる．
(1)a≦b のとき
F(a,b,n)=floor(a/(n+1))+floor(-a/(n+1))-floor((a-1)/(n+1))-floor((1-a)/(n+1)).
(2)a＞b のとき
F(a,b,n)=floor(a/(n+1))+floor(-a/(n+1))-floor((a-1)/(n+1))-floor((1-a)/(n+1))
+Σ[j=0..a-b-1]Σ[p=0..floor((a-b-1-j)/n)]binomial(j+b+1,p)*binomial(a-1-n*p,j+b)*(-1)^(j+b+p).
本問は，F(2023,2023,n)=1 となるような最小のnを求める問題ということになります．
F(a,b,n)の具体的な値をいくつか計算してみました．
F(2050,2023,6)=-262877306121254666979471832379830786015159801465595404785498,
F(2200,2100,6)=8271661316257607449154173726058504365362866144570518123012684
0027788958134867530802649500072698625282687140571413964147152231384260965009
0691998918061926152180355319776377615,
F(3000,2500,7)=2875952209866737578251128491852693833159214287218201301938788
1209469495169348882423332356060840899284449752216841849268690126137495717355
6561012589191880123863457523760261974281670712997166735211025461508809476193
9306716679969413793430081108701262651158566893304513446422502951551847386443
3864638542831789656248581400184930404821368218218993997885143805111049085673
9358082022604853938889170498975613276448925109614366800564141416406992923714
0311511572025858003810166613292201235670479198647641170312211866887763119034
67368967882207942151932014551503377863904380771905355223890963802126.
(以上)
NO6「kasama」
3/17
16時15分 受信 更新 3/31
寄せられた問題の解答です
追加問題１の与式は、
(n-18)*(n^2+18*n+324) = (m-17)*(m^2+19*m+224)
(n+118)*(n^2-118*n+13924)=(m+119)*(m^2-117*m+13824)
と変形できるので、(m,n)=(17,18),(-119,-118)が整数解には違いないのですが、それでがすべてかどうかがわかっていません。
追加問題２の2023次の係数は、プログラムで調べると、
n=1のとき-1
n=2のとき0
n=3のとき0
n=4のとき0
n=5のとき-1
n=6のとき1
となるので、n=6が答えと思われます。ただ、実直にΣを計算して、答えを導く計算過程は、とても素手でできるようなものではありません。きっと上手いやり方があるのだろうと思い、ずっと悩み続けております。
「kasama」
3/20
02時11分 受信 更新 3/31
寄せられた解答です
「kasama」
3/29 17時06分 受信 更新 3/31
追加問題１,２を再考した解答です
前回と同じ
NO7「よふかしのつらいおじさん」 3/24 18時42分 受信 更新
3/31
「よふかしのつらいおじさん」 3/25 17時19分
受信 更新 3/31
寄せられた追加問題１の解答です
NO8「三角定規」 3/３0 13時17分 受信 更新 3/31
寄せられた問題の解答です。
「水の流れ」 受信 更新 3/31
文献 算法点竄初學抄附録 国書データーベース （第51巻51oｆ63）解義
問題１に関して 「青空学園数学科」デカルトの円定理を参照。
https://aozoragakuen.sakura.ne.jp/taiwa/taiwaNch03/enteiri/node2.html
問題２に関して「高校数学の美しい物語」ベクトルを用いたオイラーの定理を
参照。 https://manabitimes.jp/math/580
問題３の解法は割愛
問題４（１）３辺ＤＥ，ＥＦ，ＦＤは図のような３つの直角三角形の斜辺となる。
よって、求める表面積は一辺が７の正方形の面積から（３＋４）２＝４９
（２）の解法は割愛
（３）の解法は割愛
過去の第268回「四面体の内接球」応募解答を参照ください。
第300回「立体の埋め込み」応募解答を参照ください。
第301回「特殊な四面体」応募解答を参照ください。
皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。
